技術士試験(情報工学部門)・情報技術者試験。ファーストマクロ。

�V−２

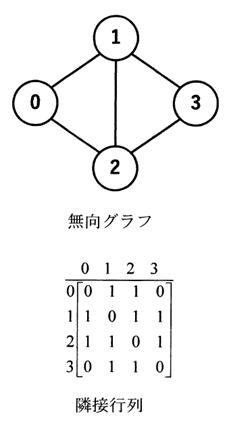
以下の無向グラフと隣接行列において、0から3へ至るパスを検索するプログラムを考える。下線部の【ア】に入るプログラム片のうち、最も適切なものはどれか。


〔プログラム〕
mm=[[0, 1, 1, 0], [1, 0, 1, 1], [1, 1, 0, 1], [0, 1, 1, 0]]
def gsearch(l, r):
　for i, c in enumerate(l):
　　if 　　　　【ア】　　　　
　　　if i==3:
　　　　print(r+[i])
　　　else:
　　　　gsearch(mm[i], r+[i])
gsearch(mm[0], [0])

〔実行結果〕
[0, 1, 2, 3]
[0, 1, 3]
[0, 2, 1, 3]
[0, 2, 3]

---

正解

�C

---

解説

隣接行列は、頂点同士が辺でつながっているかどうかを表す行列である。
例えば、頂点0の隣接行列は、頂点1と頂点2につながっているので、
[0, 1, 1, 0]と表せる。

0から3へ至るパスは以下の4通りある。
0 ⇒ 1 ⇒ 2 ⇒ 3
0 ⇒ 1 ⇒ 3
0 ⇒ 2 ⇒ 1 ⇒ 3
0 ⇒ 2 ⇒ 3
これらを正しく出力できるようにプログラムを考える。


配列mmが定義され、次に
def gsearch(l, r)
　〜
　　gsearch(mm[i], r+[i]) で
引数が l と r の関数grearch()を定義する。

プログラムは
gsearch(mm[0], [0]) から実行し、gsearch()内で再帰的に呼び出される。

なお、enumerate()関数は for文でインデックスと要素を同時に取得する関数である。for i, c in enumerate(l): によって、引数のmmのリストを i と c に以下のように 取り出していく。
mm[0]のとき: (i, c) ⇒ (0, 0), (1, 1), (2, 1), (3, 0)

また、r+[i]は、リスト r の最後に i を加えたリストとなる。

これらを踏まえ、gsearch(mm[0], [0]) をトレースすると次のようになる。

for 1回目　(r=[0])
　(i, c) = (0, 0)
　　ここで、c = 0ということは隣接していないため、処理する必要がない。また、リストr の中に自分自身や、すでに検索した点があれば、処理する必要がない。この時点で 正解は�Cと予想できる。

for 2回目　(r=[0])
　(i, c) = (1, 1)　・・・ 0が1と隣接していることが分かる。
　gsearch(mm[1], [0]+[1]) = gsearch(mm[1], [0, 1])
　　for 1回目 (r = [0, 1])
　　　(i, c) = (0, 1)　・・・i = 0がリスト r の中にある。
　　for 2回目 (r = [0, 1])
　　　(i, c) = (1, 0)
　　for 3回目 (r = [0, 1])
　　　(i, c) = (2, 1)
　　　　gsearch(mm[2], [0, 1]+[2])
　　　　 　　for 1回目 (r = [0, 1, 2])
　　　　　　　(i, c) = (0, 1)
　　　　 　　for 2回目 (r = [0, 1, 2])
　　　　　　　(i, c) = (1, 1)
　　　　 　　for 3回目 (r = [0, 1, 2])
　　　　　　　(i, c) = (2, 0)
　　　　 　　for 4回目 (r = [0, 1, 2])
　　　　　　　(i, c) = (3, 1)
　　　　　　　　print([0, 1, 2]+[3]) ・・・[0, 1, 2, 3]を出力
　　for 4回目 (r = [0, 1])
　　　(i, c) = (3, 1)
　　　　print([0,1]+[3]) ・・・[0, 1, 3]を出力
for 3回目　(r=[0])
　(i, c) = (2, 1)
　gsearch(mm[2], [0]+[2]) = gsearch(mm[2], [0, 2])
　　for 1回目 (r = [0, 2])
　　　(i, c) = (0, 1)
　　for 2回目 (r = [0, 2])
　　　(i, c) = (1, 1)
　　　　gsearch(mm[1], [0, 2]+[1])
　　　　 　　for 1回目 (r = [0, 2, 1])
　　　　　　　(i, c) = (0, 1)
　　　　 　　for 2回目 (r = [0, 2, 1])
　　　　　　　(i, c) = (1, 0)
　　　　 　　for 3回目 (r = [0, 2, 1])
　　　　　　　(i, c) = (2, 1)
　　　　 　　for 4回目 (r = [0, 2, 1])
　　　　　　　(i, c) = (3, 1)
　　　　　　　　print([0, 2, 1]+[3]) ・・・[0, 2, 1, 3]を出力
　　for 3回目 (r = [0, 2])
　　　(i, c) = (2, 0)
　　for 4回目 (r = [0, 2])
　　　(i, c) = (3, 1)
　　　　print([0,2]+[3]) ・・・[0, 2, 3]を出力
for 4回目　(r=[0])
　(i, c) = (3, 0)
　　　　　

�V−１

目次

�V−３

---